Question

Revenue from Monorail Service, Las Vegas In 2005 the Las Vegas monorail charged $3 per ride and had an average ridership of about 28,000 per day. In December 2005 the Las Vegas Monorail Company raised the fare to $5 per ride, and average ridership in 2006 plunged to around 19,000 per day.

a. Use the given information to find a linear demand equation.
b. Find the price the company should have charged to maximize revenue from ridership. What is the corresponding daily revenue?
c. The Las Vegas Monorail Company would have needed $44.9 million in revenues from ridership to break even in 2006. Would it have been possible to break even in 2006 by charging a suitable price?

Answer 1

A)The required linear demand equation ( q ) = -4500p + 41500

B) $4.61

$95680.55

C) No it would not have been possible by charging a suitable price

Explanation:

A) find the linear demand equation

given two points ; ( 3, 28000 ) and ( 5, 19000 )

slope ( m ) = ( y2 - y1 ) / ( x2 - x1 )

= ( 19000 - 28000 ) / ( 5 - 3 ) = -4500

slope intercept is represented as ; y = mx + b

where y( 28000) = -4500(3) + b

hence b = 41500

hence ; y = -4500x + 41500

The required linear demand equation ( q ) = -4500p + 41500 ----- ( 1 )

p = price per ride

B ) Determine the price the company should charge to maximize revenue from ridership and corresponding daily revenue

Total revenue ( R ) = qp

= p ( -4500p + 41500 )

hence R = -4500p^2 + 41500p ------ ( 2 )

To determine the price that should maximize revenue from ridership we will equate R = -4500p^2 + 41500p to a quadratic equation R(p) = ap^2 + bp + c

where a = -4500 , b = 41500 , c = 0

hence p =
`-(b)/(2a)` =
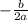`- (41500)/(2(-4500))` = 4.61

$4.61 is the price the company should charge to maximize revenue from ridership

corresponding daily revenue = R = -4500p^2 + 41500 p

where p = $4.61

hence R = -4500(4.61 )^2 + 41500(4.61) = $95680.55

C) No it would not have been possible by charging a suitable price