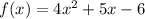Question

What is the equation in standard form of a parabola that models the values in the table

Answer 1

to solve this, you can do it the easy way or hard way

easy way is to know some stuff about parabolas and zeroes

hard way is to subsitute for x and f(x) and solve for a,b, and c with a system of 3 variables (harder)



I'm going to do the easy way
nice we are given some zeroes

when f(x)=0, x=-2
since it is quadratic, it is 2nd degree and we can write all 2nd degree functions in the form f(x)=a(x-b)(x-c)
where a is some random constant and b and c are the x intercepts
we are given that when f(x)=0, x=-2, that means one x intercept is at -2
so lets say b=-2
f(x)=a(x-(-2))(x-c)
f(x)=a(x+2)(x-c)
great, now to find the other values
when x=0, y=-6
subsitute 0 for x and see what happens
-6=a(0+2)(0-c)
-6=a(2)(-c)
-6=-2ac
divide by -2 both sides
3=ac
cool
we revisit our equation
f(x)=a(x+2)(x-c)
now if we solve for a, we can do
3=ac, a=3/c, subsitute 3/c for a
f(x)=(3/c)(x+2)(x-c)
subsitute (4,78)
78=(3/c)(4+2)(4-c)
78=(3/c)(6)(4-c)
divide both sides by 6 for ease
13=(3/c)(4-c)
13=12/c-3
add 3 to both sides
16=12/c
multiply both sides by c
16c=12
divide both sides by 16
c=12/16
c=0.75
find a
a=3/c
a=3/0.75
a=4
if might be best to leave in fraction form
a=4
c=0.75=3/4

the equation is

`f(x)=4(x+2)(x-(3)/(4))`
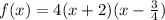
in standard form as in ax^2+bx+c form

`f(x)=4x^2+5x-6`

Answer 2

f(x) = 4x^2 + 5x -6

Explanation:

We are given with table of values

Standard form of parabola equation is

f(x)=ax^2 +bx+c

Plug in the values given in the table and make three equations

Then solve for a,b,c

x=-2 , f(x) = 0

So equation becomes
`0= a(-2)^2+b(-2)+c`

4 a - 2 b + c=0 --------> equation 1

x=0 , f(x) = -6

So equation becomes
`-6= a(0)^2+b(0)+c`

c= -6

x=4 , f(x) = 78

So equation becomes
`78= a(4)^2+b(4)+c`

16 a + 4 b + c=78--------> equation 2

We got c=-6, plug in -6 in both equations 1 and 2

4 a - 2 b - c =0--------> equation 1

4a - 2 b = 6 --------------> equation 3

16 a + 4 b + c=78--------> equation 2

16 a + 4 b = 78+6

16 a + 4 b = 84 ------------> equation 4

Multiply the third equation by 2

4a - 2 b = 6 --------------> equation 3

8a - 4b = 12

16 a + 4 b = 84 ------------> equation 4 (add the above equation)

------------------------------------

24a = 96

Divide both sides by 24

so a= 4

Now plug in 4 for 'a' in equation 3

4a - 2 b = 6

4(4) -2b= 6

16 - 2b = 6

subtract 16 on both sides

-2b = -10

Divide both sides by -2

So b= 5

Hence a= 4, b=5 and c= -6

Standard form of parabola equation is

f(x)=ax^2 +bx+c

f(x) = 4x^2 + 5x -6