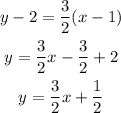As a first step to implicit differentiation, we are going to differentite both sides of the equation:
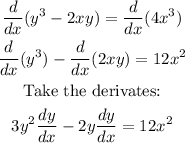
Now, we are going to keep the terms with dy/dx on the left and move the remaining terms to the right:

The equation of the tangent line can be find by substituing (1, 2) into the expression dy/dx, to find the slope:
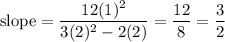
Using the point given and the slope we just calculate, we can find the equation in the point-slope form and then solve for y to give the general equation: