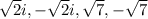Question

Hat are the solutions of the equation x4 – 5x2 – 14 = 0? Use factoring to solve.

Answer 1

-7 and 2 are factors of -14, and they make a sum of -5, therefore:
(x^2-7)(x^2+2)=0
x^=7 or x^=-2
x=√7 or-√7, x=√2i or x=-√2i

Answer 2

We are given equation:
`x^4-5x^2-14 = 0`.

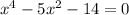Now, we need to find the solutions of the given equation.

We need to solve given equation by factoring.

`\mathrm{Rewrite\:the\:equation\:with\:}u=x^2\mathrm{\:and\:}u^2=x^4`

`u^2-5u-14=0`

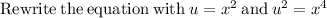
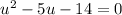
Let us factor the quadratic.

`\mathrm{Break\:the\:expression\:into\:groups}`

`=\left(u^2+2u\right)+\left(-7u-14\right)`

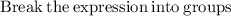
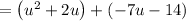
Factoring out GCF of each group.

`=u\left(u+2\right)-7\left(u+2\right)`

`\mathrm{Factor\:out\:common\:term\:}u+2`

`=\left(u+2\right)\left(u-7\right)`

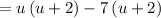
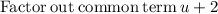
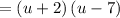
Substituting back
`u=x^2`.

`\left(x^2+2\right)\left(x^2-7\right)=0`

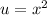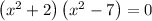
Applying zero product rule.

`x^2+2=0`

`x^2=-2`=>
`x=√(-2)`
`=√(2)i, -√(2)i`.

`x^2-7=0`

`x^2=7`=>
`x=√(7)`
`=√(7), -√(7)`.

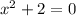
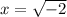
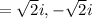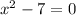
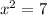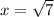
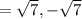Therefore, solutions of the equation are:

`√(2)i, -√(2)i,√(7), -√(7)`