Question

Look at points C and D on the graph: Coordinate grid shown from negative 6 to positive 6 in increments of 1 on both the axes. A line is drawn by connecting point C at negative 2, 0 and point D at 3, 5 What is the distance (in units) between points C and D? Round your answer to the nearest hundredth.

2.24
3.16
6.40
7.07

Answer 1

Let's see...

`d= \sqrt{(3-(-2))^(2) + (5-0)^2} \\ d=\sqrt{(5)^(2)+(5)^(2)} \\ d=√(25+25) \\ d=√(50) \\ d=7.071, or 7.07`

Answer 2

Answer: 7.07 units.

Explanation:

The distance between any two point (a,b) and (c,d) on coordinate plane is given by :-

`\text{Distance=}√((d-b)^2+(c-a)^2)`

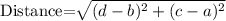
By considering the given information , we have

C= (-2,0) and D = (3,5)

Then, the distance (in units) between points C and D will be :

`CD=√((5-0)^2+(3-(-2))^2)`

`\Rightarrow\ CD=√((5)^2+(3+2)^2)`

`\Rightarrow\ CD=√(25+25)`

`\Rightarrow\ CD=√(50)=7.07106781187\approx7.07`

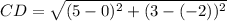
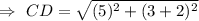
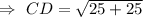
[Rounded to the nearest hundredth]

Hence, the distance (in units) between points C and D = 7.07 units.