Question

Which of the following describes how to graph the line whose equation is y = 2/3 x - 1?

A. Plot the point (0, -1), move up 3 and right 2, plot the point, and draw the line through these 2 points.
B. Plot the point (0, -1), move up 2 and right 3, plot the point, and draw the line through these 2 points.
C. Plot the point (-1, 0), move up 2 and right 3, plot the point, and draw the line through these 2 points.

Answer 1

I'm answering a bit late, but your answer should be B.) Plot the point (0, -1), move up 2 and right 3, plot the point, and draw the line through these 2 points.

Hopefully this helps!

Answer 2

Option: B is the correct answer.

B. Plot the point (0, -1), move up 2 and right 3, plot the point, and draw the line through these 2 points.

Explanation:

The equation of a line is given by:

`y=(2)/(3)x-1`

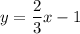
A)

Plot the point (0, -1), move up 3 and right 2, plot the point, and draw the line through these 2 points.

Now when we move up 3 units and 2 units to the right then the point is: (2,2)

This means that the graph of the function must pass through (2,2)

when x=2 then the value from the actual function is:

`y=(2)/(3)* 2-1\\\\\\y=(4-3)/(3)\\\\\\y=(1)/(3)\\eq 2`

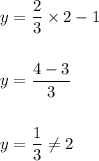
Hence, option: A is incorrect.

C)

Plot the point (-1, 0), move up 2 and right 3, plot the point, and draw the line through these 2 points.

This means that the equation of the line must pass through (-1,0) and (2,2)

Now when x= -1 we have:

`y=(2)/(3)* (-1)-1\\\\\\y=(-2-3)/(3)\\\\\\y=(-5)/(3)\\eq 0`

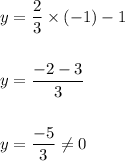
Hence, option: C is incorrect.

B)

Plot the point (0, -1), move up 2 and right 3, plot the point, and draw the line through these 2 points.

i.e. the line must pass through (0,-1) and (3,1)

Now we find the equation of a line using the two points as:

`y-b=(d-b)/(c-a)* (x-a)`

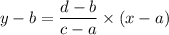
where (a,b) and (c,d) are the passing through points.

Here (a,b)=(0,-1) and (c,d)=(3,1)

Hence, we have the equation of line as:

`y-(-1)=(1-(-1))/(3-0)* (x-0)\\\\\\y+1=(2)/(3)x\\\\\\y=(2)/(3)x-1`

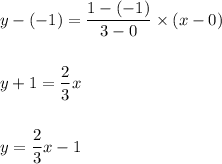
Hence, it matches the actual equation of the line.

Hence, option: B is the correct answer.