Answer:
a) k = Mg / d , b) v = √2gh , c) v_{f} =
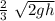 , d) x² + 6d x -
, d) x² + 6d x -
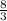 dh = 0
dh = 0
e)the spring must compress a greater distance.
Step-by-step explanation:
a) when the block of mass M is placed on the spring, we have an equilibrium condition,
∑ F = 0
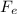 - W = 0
- W = 0
k d = Mg
k = Mg / d
b) let's use the concepts of energy to find the velocity of the block just before the collision
starting point. Position when released
Em₀ = U = m g h
lowest point. Right at the point of shock
 = K = ½ m v²2
= K = ½ m v²2
as there is no friction, energy is conserved
Em₀ = Em_{f}
mg h = ½ m v²
v = √2gh
c) The velocity of the two blocks after the collision, we define a system formed by the two blocks, in such a way that the forces during the collision are internal and the moment is conserved
initial instant. Just before the crash
p₀ = 2M v + M 0
final instant. Just after the shock, before the spring compression begins
p_{f} = (2M + M) v_{f}
the moment is preserved
p₀ = p_{f}
2M v = 3M v_{f}
v_{f} = ⅔ v
v_{f} =
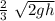
d) now we work with the joined system after the collision, let's use the concepts of energy
starting point. After shock, before beginning spring compression
Em₀ = K = ½ (3M)
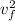
Em₀ = 3/2 M (\frac{2}{3} \ \sqrt{2gh})²
Em₀ = 4/3 M gh
final point. With the spring fully compressed
Em_f = K_e + U = ½ k x² + (3M) g x
in this case we have taken the zero of gravitational potential energy at the point where the blocks collide, as there is no friction, the energy is conserved
Em₀ = Em_f
4/3 M g h = ½ k x² + 3M g x
½ k x² + 3Mg x - 4/3 Mgh = 0
we substitute the expression for k
 (
(
 ) x² + 3Mg x -
) x² + 3Mg x -
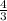 Mgh = 0
Mgh = 0
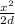 + 3 x -
+ 3 x -
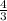 h = 0
h = 0
to find the value of the spring compression, the second degree equation must be solved
x² + 6d x -
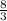 dh = 0
dh = 0
x = [-6d ±
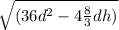 ] / 2
] / 2
x = [-6d ± 6d
 ]/2
]/2
x = 3d ( -1±
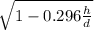 )
)
e) If the collision elastic force would not lose any part of the kinetic energy during the collision, therefore the speed of the block of mass M would be much higher and therefore the spring must compress a greater distance.