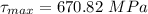Answer:
Step-by-step explanation:
Given that:
![[\sigma] = \left[\begin{array}{cc}800&300\\ \\300&-400\end{array}\right] (MPa)](https://img.qammunity.org/2022/formulas/engineering/college/75bc0tnm22czqb431cnjfwgyvurtnnagcg.png)
![[\sigma] = \left[\begin{array}{cc}\sigma_(xx)&\sigma_(xy)\\ \\\sigma_(yx)&\sigma_(yy)\end{array}\right]](https://img.qammunity.org/2022/formulas/engineering/college/gzj40f6v7tnkuvr1pc9g70oikuzzyo9nu5.png)
Using Determinant method
The principal stress is the maximum or minimum normal stress acting on any plane. For the 2D stress system, the 2-principle plane always carries zero shear stress.
For principal stress

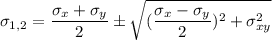

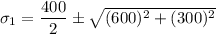
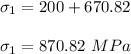
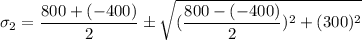
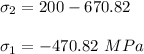
According to Mohr's circle;
Mohr's circle is the locus provided that the position of the normal stress and the shear stress is acting on any plane.
Center = (a,0)
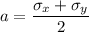
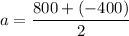
a = 200 MPa
radius (r) =

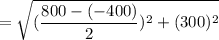
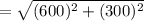
r = 670.82 MPa
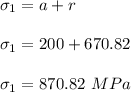
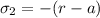 (it is negative because of the negative x-axis)
(it is negative because of the negative x-axis)