Question

F(x,y) = x^2+y^2+x^2y+6 find the absolute max and min

Answer 1

`f(x,y)=x^2+y^2+x^2y+6` has critical points where the partial derivatives simultaneously vanish:


`f_x=2x+2xy=2x(1+y)=0\implies x=0\text{ or }y=-1`

`f_y=2y+x^2=0`

`x=0\implies 2y=0\implies y=0`

`y=-1\implies-2+x^2=0\implies x=\pm\sqrt2`

So we have three critical points to consider,
`(0,0)`,
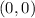
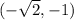
`(-\sqrt2,-1)`, and
`(\sqrt2,-1)`.

The function has Hessian


`\mathbf H(x,y)=\begin{bmatrix}f_(xx)&f_(xy)\\f_(yx)&f_(yy)\end{bmatrix}=\begin{bmatrix}2+2y&2x\\2x&2\end{bmatrix}`

At the critical points, we have


`|\mathbf H(0,0)|=\begin{vmatrix}2&0\\0&2\end{vmatrix}=4>0`

`f_(xx)(0,0)=2>0`

which means there is a minimum at (0, 0) of
`f(0,0)=6`;


`|\mathbf H(-\sqrt2,-1)|=\begin{vmatrix}0&-2\sqrt2\\-2\sqrt2&2\end{vmatrix}=-8<0`

which means
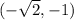
`(-\sqrt2,-1)` is a saddle point; and


`|\mathbf H(\sqrt2,-1)|=\begin{vmatrix}0&2\sqrt2\\2\sqrt2&2\end{vmatrix}=-8<0`

which means
`(\sqrt2,-1)` is also a saddle point.