the standard form of the quadratic function that meets the given conditions is:
![\[ y = x^2 - 8x + 21 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/i3a76ld1j1releb3llso.png)
Therefore, the answer is option B.
To find the standard form of the quadratic function
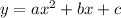 that has a vertex at
that has a vertex at
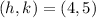 and passes through the point
and passes through the point
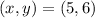 , we can use the vertex form of a quadratic function and then convert it to standard form. The vertex form of a quadratic function is:
, we can use the vertex form of a quadratic function and then convert it to standard form. The vertex form of a quadratic function is:
![\[ y = a(x - h)^2 + k \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/j212fbcvi0lvm11ew83l.png)
Given the vertex
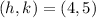 , we have:
, we have:
![\[ y = a(x - 4)^2 + 5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8prm8t9os77i7p0ohmoj.png)
Now we need to determine the value of \(a\) using the point \((5, 6)\):
![\[ 6 = a(5 - 4)^2 + 5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/i15bewtdegjdavorv8l9.png)
![\[ 6 = a(1)^2 + 5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/eneplhx4yno2dlx85l03.png)
![\[ a = 6 - 5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/577pl6pul2ukkivi9s3w.png)
![\[ a = 1 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ksv36dlrl2rf8f0xxedp.png)
So the equation in vertex form is:
![\[ y = (x - 4)^2 + 5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/zeq8iqf24g87udag306u.png)
To convert this to standard form, we expand the squared term:
![\[ y = (x^2 - 8x + 16) + 5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/gda9yk721wmifjzut5n8.png)
![\[ y = x^2 - 8x + 21 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/i3a76ld1j1releb3llso.png)
Thus, the standard form of the quadratic function that meets the given conditions is:
![\[ y = x^2 - 8x + 21 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/i3a76ld1j1releb3llso.png)
Therefore, the answer is option B.