Question

A train starts from rest at station A and accelerates at 0.6 m/s^2 for 60 s. Afterwards it travels with a constant velocity for 25 min. It then decelerates at 1.2 m/s^2 until it is brought to rest at station B. Determine the distance between the stations.

Answer 1

The distance between the station A and B will be:

`x_(A-B)=55.620\: km`

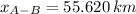
Step-by-step explanation:

Let's find the distance that the train traveled during 60 seconds.

`x_(1)=x_(0)+v_(0)t+0.5at^(2)`

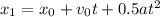
We know that starts from rest (v(0)=0) and the acceleration is 0.6 m/s², so the distance will be:

`x_(1)=(1)/(2)(0.6)(60)^(2)`

`x_(1)=1080\: m`

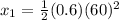
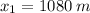
Now, we need to find the distance after 25 min at a constant speed. To get it, we need to find the speed at the end of the first distance.

`v_(1)=v_(0)+at`

`v_(1)=(0.6)(60)=36\: m/s`

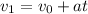
Then the second distance will be:

`x_(2)=v_(1)*1500`

`x_(2)=(36)(1500)=54000\: m`

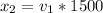
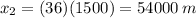
The final distance is calculated whit the decelerate value:

`v_(f)^(2)=v_(1)^(2)-2ax_(3)`

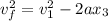
The final velocity is zero because it rests at station B. The initial velocity will be v(1).

`0=36^(2)-2(1.2)x_(3)`

`x_(3)=(36^(2))/(2(1.2))`

`x_(3)=540\: m`

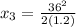
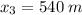
Therefore, the distance between the station A and B will be:

`x_(A-B)=x_(1)+x_(2)+x_(3)`

`x_(A-B)=1080+54000+540=55.620\: km`

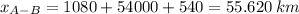
I hope it helps you!