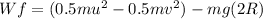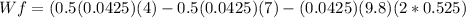Question

A small block with mass 0.0425 kg slides in a vertical circle of radius 0.525 m on the inside of a circular track. During one of the revolutions of the block, when the block is at the bottom of its path, point A, the magnitude of the normal force exerted on the block by the track has magnitude 4.05 N. In this same revolution, when the block reaches the top of its path, point B, the magnitude of the normal force exerted on the block has magnitude 0.660 N.

Required:
How much work was done on the block by friction during the motion of the block from point A to point B?

Answer 1

`W=-0.501075J \approx -0.5J`

Step-by-step explanation:

From the question we are told that

Mass of block
`M=0.425kg`

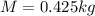
Radius of circle
`r=0.525m`

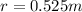
Force of track
`F_t=4.05N`

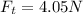
Normal Force on block
`F_n=0.660`

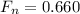
Generally the equation for Velocity of block is mathematically Given by the law of conservation of energy

`4.05=(0.425kg*9.8)+(0.425kg*v^2)/0.525`

`v=\sqrt{(0.525*(4.05-(0.0425*9.8))/(0.0425) }`

`V=-6.69 \approx 7m/s`

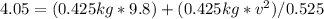
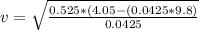
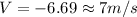
For initial velocity

0.660 = 0.0425 x u^2/0.525 - 0.0425 x 9.8

`v=\sqrt{0.525*((0.660+(0.0425*9.8))/(0.0425) }`

`V=-3.646 \approx 4m/s`

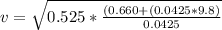
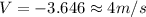
Generally the equation for work done is mathematically Given by

`Wf=(0.5mu^2 - 0.5mv^2) -mg(2R)`

`Wf=(0.5(0.0425)(4) - 0.5(0.0425)(7) -(0.0425)(9.8)(2*0.525)`

`W=-0.501075J \approx -0.5J`