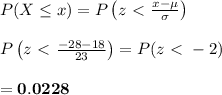Question

A security with normally distributed returns has an annual expected return of 18% and a standard deviation of 23%. the probility of getting a return of -28% or lwer in any one year is

Answer 1

The probability that a randomly selected data from a normally distributed dataset with mean of μ, and standard deviation of σ, is less than a value x is given by:


`P(X\leq x)=P\left(z\ \textless \ (x-\mu)/(\sigma) \right)`

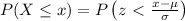
Given that a security with normally distributed returns has an annual expected return of 18% and a standard deviation of 23%.


`\mu=18\% \\ \\ \sigma=23\%`

The probability of getting a return of -28% or lower in any one year is given by:


`P(X\leq x)=P\left(z\ \textless \ (x-\mu)/(\sigma) \right) \\ \\ P\left(z\ \textless \ (-28-18)/(23) \right)=P(z\ \textless \ -2) \\ \\ =\bold{0.0228}`