Question

A random sample of 600 voters in a particular city found 102 voters who voted yes on proposition 200. find a 95% confidence interval for the true percent of voters in this city who voted yes on proposition 200. express your results to the nearest hundredth of a percent.

Answer 1

n = 600, the sample size

Because 102 voters said 'Yes' to the proposition, the sample proportion is

`\hat{p} = (102)/(600) =0.17 \\ 1 - \hat{p} = 1-0.17 = 0.83`

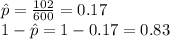
The standard error is

`SE_(p) = \sqrt{ \frac{\hat{p}(1-\hat{p})}{n} } = \sqrt{ ((0.17)(0.83))/(600) } = 0.0153`

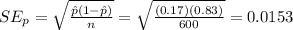
The confidence interval is

`\hat{p} \pm z^(*) SE_(p)`

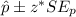
From tables, z* = 1.96 at the 95% confidence level.
Therefore the confidence interval is

`0.17 \pm 1.96(0.0153) = (0.14, 0.20)`

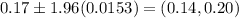
Answer: (0.14, 0.20)