Jim has only dimes and nickels in his coin bank. He has 37 coins with a total value of $2.65. How many nickels are in Jim’s coin bank? Enter your answer in the box.

Question

asked Jul 7, 2018 234k views

2 Answers

Mwhuss · Answer 1 · 2018-07-10T19:41:16+0000

Answer:

21

Explanation:

Let x represent the number of dimes and y represent the number of nickels. The total number of coins is 37; this gives us the equation

x+y = 37

Each dime is worth ten cents, or 0.10, and each nickel is worth five cents, or 0.05. The total amount of money is given by

0.10x+0.05y = 2.65

This gives us the system

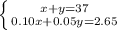
$\left \{ {{x+y=37} \atop {0.10x+0.05y=2.65}} \right.$

To solve this, we will use substitution. We will isolate x in the first equation:

x+y=37

Subtract y from each side:

x+y-y = 37-y

x = 37-y

Substitute this into the second equation:

0.10(37-y)+0.05y = 2.65

Using the distributive property,

0.10(37)-0.10(y)+0.05y = 2.65

3.70-0.10y+0.05y = 2.65

Combining like terms,

3.70-0.05y = 2.65

Subtract 3.70 from each side,

3.70-0.05y-3.70 = 2.65-3.70

-0.05y = -1.05

Divide both sides by -0.05:

-0.05y/-0.05 = -1.05/-0.05

y = 21

There were 21 nickels.