From the compound interes formula, given by
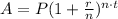
where A is the future amount, P is the principal value, r is the rate, n is the number of times interest per unit of time t, we have
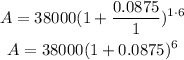
which gives
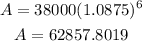
Then, since the loan is paid in full at the end of the year, we must paid back: $62,857.80