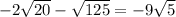Question

What is −220−−√−125−−−√ in simplest radical form?

Answer 1

`-2√(20)-√(125)=-9√(5)`

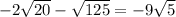
Explanation:

Given : expression
`-2√(20)-√(125)`

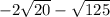
We have to write in simplest radical form for the given expression.

Consider the given expression
`-2√(20)-√(125)`

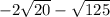
Prime factorization is a way of writing a number as the product of its primes.

Thus, 20 can be written as 2 × 2 × 5

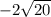`-2√(20)` can be written as
`=-2√(2^2\cdot \:5)`

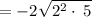
Apply radical rule,
`\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}` , we get,

`-2\cdot 2√(5)=-4√(5)`

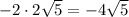
Also, 125 can be written as 5 × 5 × 5

`√(125)` can be written as
`=√(5^3)`

Apply radical rule,
`\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}` , we get,

`√(125)=5√(5)`

The given expression becomes,

`-2√(20)-√(125)=-4√(5)-5√(5)=-9√(5)`

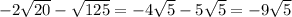
Thus,
`-2√(20)-√(125)=-9√(5)`

Answer 2

`-2 √(20) - √(125) =-2 √(4*5) -√(25*5) \\ \\ =-4√(5)-5√(5)=-9√(5) \\ \\ \therefore -2 √(20) - √(125)=-9√(5)`