Answer:
Option C is correct.
Step-by-step explanation:
Rhombus states that a parallelogram with four equal sides and sometimes one with no right angle.
Given: The coordinate of the vertices of quadrilateral ABCD are A(−6, 3) , B(−1, 5) , C(3, 1) , and D(−2, −2) .
The condition for the segment
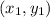 ,
,
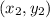 to be parallel to
to be parallel to
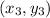 ,
,
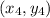 is matching slopes;
is matching slopes;
 or
or
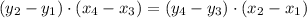 ....[1]
....[1]
So, we have to check that
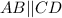 and
and
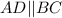
First check
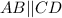
A(−6, 3) , B(−1, 5) , C(3, 1) , and D(−2, −2)
substitute in [1],
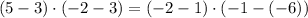
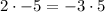
-10 ≠ -15
Similarly,
check
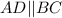
A(−6, 3) , D(−2, −2) , B(−1, 5) and C(3, 1)
Substitute in [1], we have

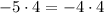
-20 ≠ -16.
Both pairs of sides are not parallel,
therefore, Quadrilateral ABCD is not a rhombus because there are no pairs of parallel sides.