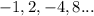Answer:
Infinite alternating sequence
Explanation:
As we know that series is basically sum of sequence, so, the given set of numbers is not an infinite arithmetic series, finite geometric series and an infinite geometric series as it is just a sequence of numbers
Now, we need to check if
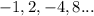 is an infinite alternating sequence or not .
is an infinite alternating sequence or not .
An infinite alternating sequence is basically of form
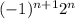
If we take
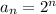
For n=0 , we get
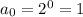
For n=1 , we get
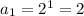
For n=2 , we get
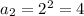
For n=3 , we get
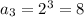 and so on
and so on
So, we get sequence as
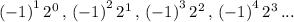
i.e