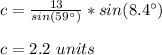Answer:
First triangle

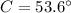
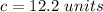
Second triangle
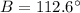

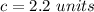
Explanation:
In this problem we have


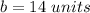
First Triangle
Step 1
Find the value of angle B
Applying the law of sines

substitute and solve for B
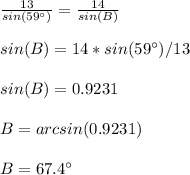
There are two measures of angle B, supplementary to each other
Step 2
Find the value of angle C
Remember that
the sum of the internal angles of a triangle is equal to

so
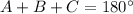
we have


substitute and solve for C
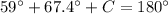
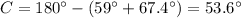
Step 3
Find the measure of side c
Applying the law of sines
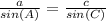
substitute and solve for c

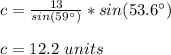
Second Triangle
Step 1
Find the value of angle B
Applying the law of sines

substitute and solve for B
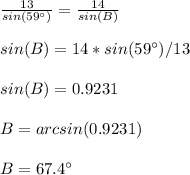
Remember that the angle B can take two values

Step 2
Find the value of angle C
Remember that
the sum of the internal angles of a triangle is equal to

so
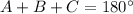
we have

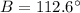
substitute and solve for C
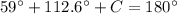

Step 3
Find the measure of side c
Applying the law of sines
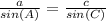
substitute and solve for c