Question

Find The art length of a sector with an area of 8 square units.

Answer 1

`\bf \textit{area of a sector of a circle}\\\\ A=\cfrac{\theta \pi r^2}{360}\quad \begin{cases} r=radius\\ \theta =angle~in\\ \qquad degrees\\ ------\\ A=8\\ r=4 \end{cases}\implies 8=\cfrac{\theta \pi 4^2}{360}\implies \cfrac{8\cdot 360}{4^2\pi }=\theta \\\\\\ \cfrac{2880}{16\pi }=\theta \implies \boxed{\cfrac{180}{\pi }=\theta }\\\\ -------------------------------\\\\`


`\bf \textit{arc's length}\\\\ s=\cfrac{\theta \pi r}{180}\quad \begin{cases} r=radius\\ \theta =angle~in\\ \qquad degrees\\ ------\\ \theta =(180)/(\pi )\\ r=4 \end{cases}\implies s=\cfrac{\frac{180}{\underline{\pi} }\underline{\pi} \cdot 4}{180}\implies s=\cfrac{\underline{180}\cdot 4}{\underline{180}} \\\\\\ \boxed{s=4}`

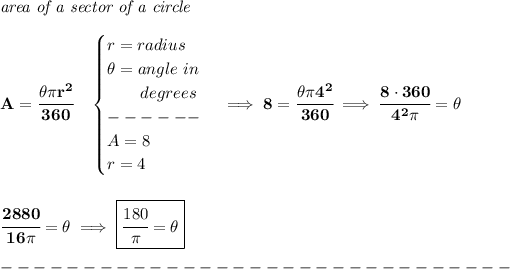
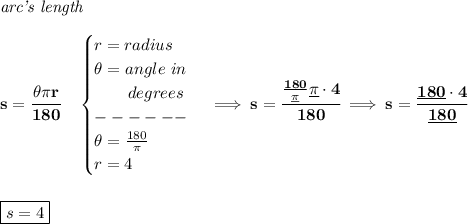
if you do a quick calculation on what that angle is, you'll notice that it is exactly 1 radian, and an angle of 1 radian, has an arc that is the same length as its radius.

that's pretty much what one-radian stands for, an angle, whose arc is the same length as its radius.