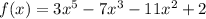Question

Use the Remainder Theorem to determine if x - 2 is a factor of the polynomial: f(x) = 3x^5 - 7x^3 - 11x^2 + 2

Answer 1

f(2)=3(2)^5 - 7(2)^3 - 11(2)^2 + 2
f(2)=(3×32)-(7×8)-(11×4) + 2
f(2)= 96 - 56 - 44 + 2
f (2)= -2

Remainder: -2

....so no its not a factor.

Answer 2

(x-2) is not a factor of
`f(x)=3x^5-7x^3-11x^2+2`

Explanation:

The Remainder Theorem: If (x-a) is a factor of the f(x) then f(a) = 0

Here,

`f(x)=3x^5-7x^3-11x^2+2`

a = 2

Hence, find f(2) and check if it is zero or not.

`f(2)=3(2)^5-7(2)^3-11(2)^2+2\\\\f(2)=3\cdot32-7\cdot8-11\cdot4+2\\\\f(2)=96-56-44+2\\\\f(2)=-2\\eq0`

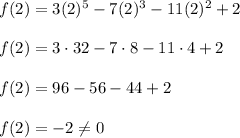
Since, f(2) is not equal to zero.

Hence, from factor theorem, (x-2) is not a factor of
`f(x)=3x^5-7x^3-11x^2+2`