Answer:
 and
and
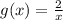
Explanation:
To prove that we have to demonstrate
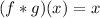
This proof is about a composition of functions, where we have to enter one function inside another, in this case,
 goes inside
goes inside
 . So if results in
. So if results in
 , then will be proved.
, then will be proved.

As you can see, the composition is to replace
 for the variable of
for the variable of
 .
.
Solving the expression:
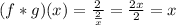
After replacing and applying the composition, we have
 as a result. Therefore, we can say that the pair of functions of option B is the answer, because they satisfy the expression given.
as a result. Therefore, we can say that the pair of functions of option B is the answer, because they satisfy the expression given.