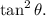Question

Simplify parenthesis 1 minus cosine theta parenthesis times parenthesis 1 plus cosine theta parenthesis divided by parenthesis 1 minus sine theta parenthesis times parenthesis 1 plus sine theta parenthesis.

sin2 θ
cos2 θ
tan2 θ
cosine theta over sine theta

Answer 1

c

Explanation:

Answer 2

The identities used to simplify the expression are the following:

The difference of squares formula,
`x^2-y^2=(x-y)(x+y)`.

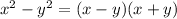
The well-known Pythagorean trig. identity,
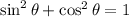
`\sin^2\theta+\cos^2\theta=1`, for any angle theta.

Last, the identity
`\displaystyle{ (\sin\theta)/(\cos\theta)=\tan\theta.`


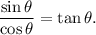
Thus, from the difference of squares identity we have


`\displaystyle{ ((1-\cos\theta)(1+\cos\theta))/((1-\sin\theta)(1+\sin\theta))= (1-\cos^2\theta)/(1-\sin^2\theta).`


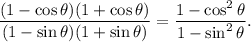
From the identity
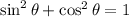
`\sin^2\theta+\cos^2\theta=1`, we have


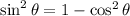
`\sin^2\theta=1-\cos^2\theta`, and
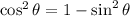
`\cos^2\theta=1-\sin^2\theta`, thus


`\displaystyle{ (1-\cos^2\theta)/(1-\sin^2\theta)= (\sin^2\theta)/(\cos^2\theta)= ((\sin\theta)/(\cos\theta))^2=\tan^2\theta.`


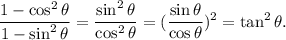
Answer:
`\tan^2\theta.`