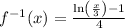Answer:
The inverse of the function
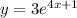 is
is
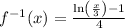
Explanation:
Given the function
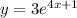 we want to find the inverse function,
we want to find the inverse function,
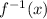
- First, replace every x with a y and replace every y with an x.
- Solve the equation from Step 1 for y.
- Replace y with
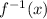 .
.
Applying the above process we get:
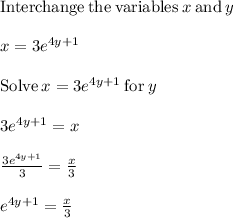
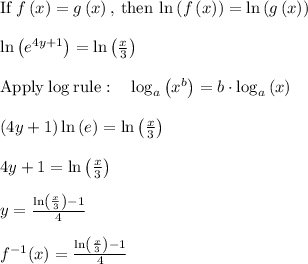
The inverse of the function
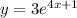 is
is