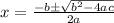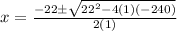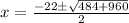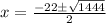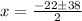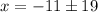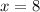Question

A pool measuring 20 meters by 24 meters is surrounded by a path of uniform

width, as shown in the figure. If the area of the pool and the path combined is
1440 square meters, what is the width of the path?

Answer 1

8

Explanation:

If the width of the path is x, then the dimensions of the combined area would be (20 + 2x) × (24 + 2x). Since the combined area is given as 1440, we can equate this with the area of a rectangle with these dimensions.

1440 = (20 + 2x)(24 + 2x)

Expand the brackets

1440 = 480 + 88x + 4x^2

Rearrange the equation, moving the 1440 to the other side so that it is equal to zero

0 = 4x^2 + 88x - 960

Divide by 4 as it is a common factor

0 = x^2 + 22x - 240

Use the quadratic formula

For an equation of the form 0 = ax^2 + bx + c, the quadratic formula is:

`x = \frac{ - b \pm \sqrt{ {b}^(2) - 4ac } }{2a}`

`x = \frac{ - 22 \pm \sqrt{ {22}^(2) - 4 (1)( - 240)} }{2(1)}`

`x = ( - 22 \pm √(484 + 960) )/(2)`

`x = ( - 22 \pm √(1444) )/(2)`

`x = ( - 22 \pm38)/(2)`

`x = - 11 \pm19`

`x = 8`