Question

A Gallup poll of 1001 Americans age 18 and over conducted in May of 2013 found that 80% of the respondents “strongly agree” that K-12 schools should teach critical thinking to children. What is the 95% confidence interval for this statistic?

Answer 1

We have:
Sample proportion, p = 80% = 0.8
Sample size, n = 1001 × 0.8 = 800.8
Population size, N = 1001
Confidence interval 95% ⇒ the z-value for this is 1.96

We'd need to work out the standard deviation (σ) and the error margin (E) in order to work out the confidence interval

σ =
`\sqrt{ (p(1-p))/(n) } * \sqrt{ (N-n)/(N-1) }`

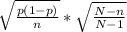
Substituting the value we have

σ =
`\sqrt{ (0.8(1-0.8))/(800.8) }* \sqrt{ (1001-800.8)/(1001-1) }`
σ =
`\sqrt{ (0.16)/(800.8) }* \sqrt{ (200.2)/(1000) }`
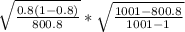
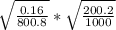
σ = 0.006325

Calculating the margin of error (E)
Standard Deviation × Critical Value = 0.006325 × 1.96 = 0.012397

So, the sample 95% interval is given as 80% ⁺/₋ 0.012 which means between 0.788 and 0.812