Question

the volume v of a right circular cylinder of radius r and heigh h is V = pi r^2 h 1. how is dV/dt related to dr/dt if h is constant and r varies with time? 2. how is dv/dt related to dh/dt if r is constant and h varies with time? 3. how is dV/dt related to dh/dt and dr/dt if both h and r vary with time?

Answer 1

In general, the volume


`V=\pi r^2h`

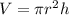
has total derivative


`(\mathrm dV)/(\mathrm dt)=\pi\left(2rh(\mathrm dr)/(\mathrm dt)+r^2(\mathrm dh)/(\mathrm dt)\right)`

If the cylinder's height is kept constant, then
`(\mathrm dh)/(\mathrm dt)=0` and we have


`(\mathrm dV)/(\mathrm dt)=2\pi rh(\mathrm dt)/(\mathrm dt)`

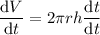
which is to say,
`(\mathrm dV)/(\mathrm dt)` and
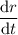
`(\mathrm dr)/(\mathrm dt)` are directly proportional by a factor equivalent to the lateral surface area of the cylinder (
`2\pi r h`).

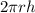
Meanwhile, if the cylinder's radius is kept fixed, then


`(\mathrm dV)/(\mathrm dt)=\pi r^2(\mathrm dh)/(\mathrm dt)`

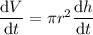
since
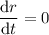
`(\mathrm dr)/(\mathrm dt)=0`. In other words,
`(\mathrm dV)/(\mathrm dt)` and
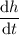
`(\mathrm dh)/(\mathrm dt)` are directly proportional by a factor of the surface area of the cylinder's circular face (
`\pi r^2`).

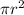
Finally, the general case (
`r` and
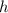
`h` not constant), you can see from the total derivative that
`(\mathrm dV)/(\mathrm dt)` is affected by both
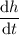
`(\mathrm dh)/(\mathrm dt)` and
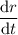
`(\mathrm dr)/(\mathrm dt)` in combination.