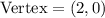Question

Use the graph of the parabola to fill in the table

Answer 1

From the question and graph provided we have a parabola (graph of a quadratic equation).

The characteristics of the graph includces amongst other things its "U" shape which clearly identifies a parabola.

ANSWER:

(a)

The parabola in this graph is an upside down "U" shaped graph which means it actually opens downwards.

(b)

The x-intercept(s) is defined as the point(s) where the parabola crosses the x-axis and at the same time the y-value is zero, that is,

`\begin{gathered} \text{When} \\ y=0,x=\text{?} \end{gathered}`

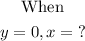
Along the horizontal line, y is always equal to zero, and at that point the graph touches the x-axis at x = 2. Therefore;

`\begin{gathered} x-\text{intercept;} \\ x=2 \end{gathered}`

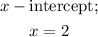
Similarly along the vertical line, x is always equal to zero, and at that point the graph touches the y-axis at y = -1. Therefore;

`\begin{gathered} y-\text{intercept;} \\ y=-1 \end{gathered}`

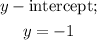
(c)

The vertex is the highest/lowest point on the parabola. That is the point where graph reaches its maximum and then begins to fall.

From the graph provided, the vertex here is at the point

`\text{Vertex}=(2,0)`