Question

Find all values of x that are simultaneously a solution to the congruences x ≡ 2 (mod 3), x ≡ 1 (mod 5), x ≡ 3 (mod 29).

Answer 1

`\begin{cases}x\equiv2\pmod3\\x\equiv1\pmod5\\x\equiv3\pmod{29}\end{cases}`

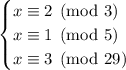
Let's start by supposing
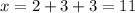
`x=2+3+3=11`. Modulo 3, we end up with 2 as needed.

But modulo 5, we want to get 1, so we'd need to multiply the first and last terms by 5 and the second term by the inverse of 3 modulo 5. We have
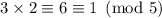
`3*2\equiv6\equiv1\pmod5`, so we multiply by 2:


`x=2*5+3*2+3*5=31`

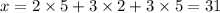
But now modulo 3, the first term gives a remainder of 1, so simply multiply by 2:


`x=2*5*2+3*2+3*5=41`

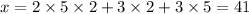
Next, modulo 29, we can force the first two terms to vanish by multiplying them by 29, but the last term still yields 15. We want to get 3 on its own, so we could just multiply the third term by the inverse of 5 modulo 29. We have
`5*6\equiv30\equiv1\pmod{29}`.


`x=2*5*2*29+3*2*29+3*5*6=844`

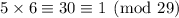
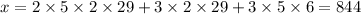
Now,
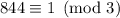
`844\equiv1\pmod3`, so we need to multiply the first term by 2 one more time;
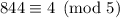
`844\equiv4\pmod5`, so we need to multiply the second term by the inverse of 4 modulo 5, which would be 4 since
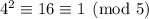
`4^2\equiv16\equiv1\pmod5`; and
`844\equiv3\pmod{29}`, so the last term is okay.


`x=2*5*2*29*2+3*2*29*4+3*5*6=1946`

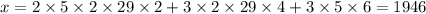
We know 1946 is a possible solution because we engineered it that way, but it's not the smallest positive solution. We have


`1946\equiv206\pmod{3*5*29}\equiv206\pmod{435}`

The general solution to the system is then
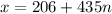
`x=206+435n`, where
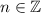
`n\in\mathbb Z`.