Question

A human is lifting their arm against the force of gravity using only the biceps brachii. The muscle inserts 0.04 m from the joint axis of rotation, and generates a force of 55 N. The mass of the forearm & hand is 1.84 kg, the center of mass is located 0.11 m from the joint axis, and the moment of inertia is 3.4 kg m2. Assume the arm is at the right angle.

Required:
a. What is the net torque at the elbow joint?
b. What is the angular acceleration of the forearm?
c, What force would the biceps need to generate to keep the hand steady?

Answer 1

a) ∑ tau = - 1.9965 N m , b) α = 0.587 rad / s², c) F₁ = 5.09 N

Step-by-step explanation:

a) the torque is given by the expression

Σ τ = Σ F x r

for this case we assume that the counterclockwise rotations are positive

In the problem, the right arm F₁ = 55 N applied at a distance x₁= 0.04m and the weight of the forearm mass W = 1.84 kg applied to x₂ = 0.11 m gives us two forces, this force has to create a rotation counterclockwise thereby creating positive torque

∑ tau = -F₁ x₁ + W x₂

∑ tau = - 55 0.04 + 1.85 0.11

∑ tau = - 1.9965 N m

b) the angular acceleration can be obtained from Newton's second law for rotations

τ = I α

α = τ/I

α = 1.9965 / 3.4

α = 0.587 rad / s²

c) what is the strength of the biceps to maintain balance

∑ τ = 0

-F₁ x₁ + W x₂ = 0

F₁ =
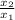`(x_(2) )/( x_(1) )` W

F₁ =
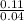`(0.11)/(0.04)` 1.85

F₁ = 5.09 N