Answer:
1
Explanation:
Given: A polynomial
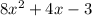 is divided by another polynomial
is divided by another polynomial

To find: Remainder when
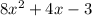 is divided by
is divided by

Solution:
To find the remainder when
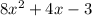 is divided by
is divided by

First, equate
 with 0.
with 0.
Now,
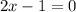
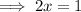
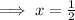
Now, to find the remainder put
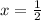 in
in
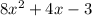
So, we have
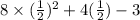
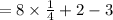


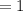
Hence, the remainder is 1.