Question

The sum of the squares of two consecutive even integers is 452. find the two integers.

Answer 1

Hi there! We can create a number equation to find your solution. Already, we know that two consecutive integers can be represented by
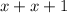
`x+x+1`. All we have to do is square that expression and make it equal to 452. This gives us:

`(x)^(2) +(x+1)^(2) =452`
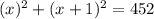
We can simplify that down to
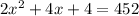
`2x^(2)+4x+4 =452`. Now, we can subtract 452 from both sides to make the whole left side equation equal to zero. Doing that gives us
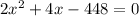
`2x^(2)+4x-448=0`. We see that 2 can be factored out of the whole equation, giving us
`2(x^(2)+2x-224)=0`. Next, we can factor the equation to get
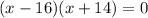
`(x-16)(x+14)=0`. We can use the Zero Product Property to find the x values of -16 and 14. Therefore, the two integers are -16 and 14. Hope this helped!

Answer 2

Hii

I m here to help u!!!


Let the two consecutive even integers are:-
x and x+2

according to the question ,we have
x^2 + (x+2)^2 =452
2x^2 + 4 + 4x =452
x^2 +2x -224=0

Now splitting the middle terms
x^2 + 16x -14x -224=0
we get
x=14
So the integers are 14 and 16.

I Hope it helps you!