At the end of 9 years, Beth will have approximately $4,051.63 in her account.
How to calculate the final amount Beth will have at the end of 9 years
To calculate the final amount Beth will have at the end of 9 years, use the formula for compound interest with semiannual compounding.
The formula is:
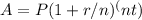
Where:
A = the future value of the investment
P = the principal amount (initial deposit)
r = annual interest rate (in decimal form)
n = number of compounding periods per year
t = number of years
In this case, Beth deposits $2000 at the end of each six-month period, which means she makes two deposits per year. The interest rate is 8% or 0.08 in decimal form, and the compounding is semiannual.
Let's calculate the future value:
P = $2000 (principal amount)
r = 0.08 (annual interest rate)
n = 2 (compounding periods per year)
t = 9 (number of years)
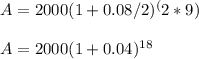
Calculating
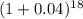 , gives approximately 2.0258165.
, gives approximately 2.0258165.
A = 2000 * 2.0258165
A ≈ $4,051.63
Therefore, at the end of 9 years, Beth will have approximately $40, 051.63 in her account. Rounded to the nearest hundredth, the final amount is $4, 051.63.