Question

To start a new business Beth deposits $2000 at the end of each six-month period in an account that pays 8%, compounded semiannually. How much will she have at the end of 9 years?

Answer 1

At the end of 9 years, Beth will have approximately $4,051.63 in her account.

How to calculate the final amount Beth will have at the end of 9 years

To calculate the final amount Beth will have at the end of 9 years, use the formula for compound interest with semiannual compounding.

The formula is:

`A = P(1 + r/n)^(nt)`

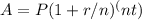
Where:

A = the future value of the investment

P = the principal amount (initial deposit)

r = annual interest rate (in decimal form)

n = number of compounding periods per year

t = number of years

In this case, Beth deposits $2000 at the end of each six-month period, which means she makes two deposits per year. The interest rate is 8% or 0.08 in decimal form, and the compounding is semiannual.

Let's calculate the future value:

P = $2000 (principal amount)

r = 0.08 (annual interest rate)

n = 2 (compounding periods per year)

t = 9 (number of years)

`A = 2000(1 + 0.08/2)^(2*9)\\\\A = 2000(1 + 0.04)^1^8`

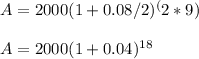
Calculating
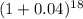`(1 + 0.04)^1^8`, gives approximately 2.0258165.

A = 2000 * 2.0258165

A ≈ $4,051.63

Therefore, at the end of 9 years, Beth will have approximately $40, 051.63 in her account. Rounded to the nearest hundredth, the final amount is $4, 051.63.

Answer 2

At the end of 9 years, Beth will have approximately $4,051.63

Explanation:

Given the following data

Principal = $2000

rate = 8%; 0.08

year = 9

Compounded semiannually

i.e n = 2

We will be using the compound interest formula

`\begin{gathered} A\text{ = P(1 + }(r)/(n))^{n\cdot\text{ t}} \\ A\text{ = 2000 (1 + }(0.08)/(2))^{2\cdot\text{ 9}} \\ A=2000(1+0.04)^(18) \\ A=2000(1.04)^(18) \\ A\text{ = 2000 }\cdot\text{ 2.02581} \\ A\text{ = \$4,051.63} \end{gathered}`

At the end of 9 years, Beth will have approximately $4,051.63