Question

If f(x) is discontinuous, determine the reason.

f(x) = {x^2 -4, x<1
          { x+4, x>1

 f(x) is continuous for all real numbers  
The limit as x approaches 1 does not exist


 f(1) does not equal the limit as x approaches 1
 f(1) is not defined

Answer 1

F(1) is not defined

Explanation:

Answer 2

The function is


`f(x) = \begin{cases} x^2-4 &\mbox{if } x\ \textless \ 1, \\ x+4 & \mbox{if } x\ \textgreater \ 1. \end{cases}`.

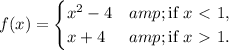
To the left of 1 the function is a quadratic polynomial, to the right, it is a linear polynomial. Polynomial functions are always continuous, so the only candidate point for discontinuity is x=1.

The left limit is calculated with 1 substituted in
`x^2+4`, which gives 5.

The right limit, is computed using the rule for the right part of 1, that is x+4.

Thus, the right limit is 1+4=5.

So, both left and right limits are equal. Now if f(1) is 5, then the function is continuous at 1.

But the function is not defined for x=1, that is x=1 is not in the domain of the function. Thus, we have a "whole" (a discontinuity) in the graph of the function.

The reason is now clear:

Answer: f(1) is not defined