Question

13+8 POINTS!!!! PLEASE HELP ME PLEASE!!!!! DUE TODAY PLEASE HELP!!!

Complete the coordinate proof of the theorem.


Enter your answers in the boxes.
The coordinates of parallelogram ABCD are A(0, 0) , B(a, 0) , C(??), and D(c, b) .

The coordinates of the midpoint of AC¯¯¯¯¯ are (, b2 ).

The coordinates of the midpoint of BD¯¯¯¯¯ are ( a+c2 , ).

The midpoints of the diagonals have the same coordinates.

Therefore, AC¯¯¯¯¯ and BD¯¯¯¯¯ bisect each other.

Answer 1

the picture below does not give specific instruction

Answer 2

Explanation:

1). Coordinates of point C will be

x - coordinates = [Distance of B from the origin + Distance of D from y axis]

= (a + c)

y - coordinates = (Distance of D from x - axis)

= b

Therefore, coordinates of C will be [(a + c), b]

2). Coordinates of the midpoint of AC =
`[((a+c)+0)/(2), (b+0)/(2)]`

=
`[((a+c))/(2), (b)/(2)]`

[Since coordinates of the midpoint of (x, y) and (x', y') are denoted by (
`(x+x')/(2),(y+y')/(2)`)]

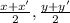3). Coordinates of the midpoint of BD =
`[((a+c))/(2), (b+0)/(2)]`

=
`[((a+c))/(2), (b)/(2)]`