Question

A direct variation function contains the points (2, 14) and (4, 28). Which equation represents the function?

Answer 1

a direct variation function, is just another way to word a "linear equation", and the slope will then be the "constant of variation".

so, in short, what's the equation of the line that runs through 2,14 and 4,28?





`\bf slope = {{ m}}= \cfrac{rise}{run} \implies \cfrac{{{ y_2}}-{{ y_1}}}{{{ x_2}}-{{ x_1}}}\implies \cfrac{28-14}{4-2}\implies \cfrac{14}{2}\implies 7 \\\\\\ % point-slope intercept \stackrel{\textit{point-slope form}}{y-{{ y_1}}={{ m}}(x-{{ x_1}})}\implies y-14=7(x-2) \\\\\\ y-14=7x-14\implies y=7x`

Answer 2

we know that

A relationship between two variables, x, and y, represent a direct variation if it can be expressed in the form
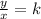`(y)/(x)=k` or
`y=kx`

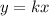
In this problem we have

Points
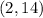`(2,14)` and
`(4,28)`

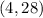
so

Find the value of k

First point

`(14)/(2)=k`

`k=7`

Second point

`(28)/(4)=k`

`k=7`

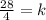
the function is

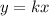`y=kx` --------> substitute the value of k

`y=7x`

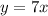
therefore

the answer is

`y=7x`

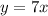
In this problem with a single point was sufficient to calculate the equation, since in a direct variation the line passes through the origin, it is not necessary to use the formula of the slope