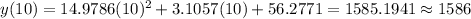Question

Year (X) =2000 2001 2002 2003 2004

Cost in Dollars(Y) = 56.25 74.30 122.75 200.00 308.50

The table shows the cost of a game from 2000 to 2004, which has been increasing in a quadratic fashion. Let x = 0 in 2000, and find the best-fit quadratic equation. What will game cost in 2010?
A) $417
B) $746
C) $960
D) $1,586

Answer 1

Here we are going to use the equation y=15x2+3x+56.
x=0 in 2,000 so x=10 in 2010.
Substitute 10 for x.
After this we have the answer: D. $1,586

Answer 2

The best-fit quadratic equation is
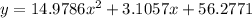`y=14.9786x^2+3.1057x+56.2771` and the game cost in 2010 will be $1586

Solution-

Plotting a table taking year as input variable and cost as output variable.

X= year - 2000

Y= cost in dollar.

Quadratic equation formula,

`y=ax^2+bx+c`

`a=\frac{(\sum x^2y\sum xx)-(\sum xy\sum xx^2)}{(\sum xx\sum x^2x^2)-({\sum xx^2)}^2}`

`b=\frac{(\sum xy\sum x^2x^2)-(\sum x^2y\sum xx^2)}{(\sum xx\sum x^2x^2)-({\sum xx^2)}^2}`

`c=(\sum y)/(n)-b(\sum x)/(n)-a(\sum x^2)/(n)`

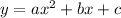
Where,

`\sum xx=\sum x^2-((\sum x)^2)/(n)`

`\sum xy=\sum xy-(\sum x\sum y)/(n)`

`\sum xx^2=\sum x^3-(\sum x\sum x^2)/(n)`

`\sum x^2y=\sum x^2y-(\sum x^2\sum y)/(n)`

`\sum x^2x^2=\sum x^4-((\sum x^2)^2)/(n)`

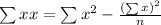
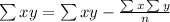
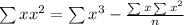
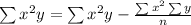
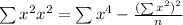
Putting the values, we get

`a=14.9786,b=3.1057,c=56.2771`

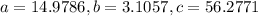
Putting these in the quadratic equation,

`y=14.9786x^2+3.1057x+56.2771`

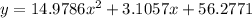
In order to get the cost of game in 2010, we can put x=10 to get the value of y or the cost of game.

`y(10)=14.9786(10)^2+3.1057(10)+56.2771=1585.1941 \approx 1586`