Question

The coordinates of the vertices of quadrilateral RSTU are R(−4, 1) , S(4, −1) , T(3, −6) , and U(−5, −4) . Which statement correctly describes whether quadrilateral RSTU is a rectangle?

Answer 1

For k12- the answer is Quadrilateral RSTU is not a rectangle because it has no right angles.

Explanation:

Answer 2

Solution: A quadrilateral RSTU whose vertices are R(−4, 1) , S(4, −1) , T(3, −6) , and U(−5, −4).

RS =
`\sqrt{(4+4)^(2)+(-1-1)^(2)} =√(64+4)= √(68)`

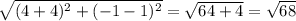
ST=
`\sqrt{(4-3)^(2)+(-1+6)^(2)}= √(1+25) =√(26)`

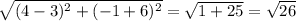
TU=
`\sqrt{(3+5)^(2)+(-6+4)^(2)}= √(64+4)= √(68)`

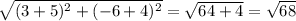
UR =
`\sqrt{(-5+4)^(2)+(-4-1)^(2)}= √(1+25) =√(26)`

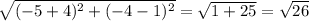
→RS=TU, and ST=UR⇒ Opposite sides are equal.

Slope of RS =
`(-1-1)/(4+4) = (-2)/(8)=  (-1)/(4)`

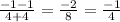
Slope of TS=
`(-6+1)/(3-4) =(-5)/(-1)=5`

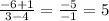
Slope of RS × Slope of TS = -1/4 × 5 = -5/4 ≠ -1, So lines are not perpendicular.

∴ quadrilateral RSTU is not a rectangle.