Question

(Lesson 11.1) Solve each system of equations by graphing. (1 point each)s y = x +312x + y = -61.1-8 -6

Answer 1

It is required to solve the following system of equations by graphing:

`\begin{cases}y={x+3} \\ 12x+y=-6{}\end{cases}`

To do this, graph each line on the same coordinate plane, and find the point of intersection of the lines.

Graph the first line, y=x+3:

Find two points that satisfy the equation of the line.

Substitute x=0 into the first equation and find the value of y:

`y=0+3=3`

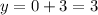
Hence, the line passes through the point (0,3).

Substitute x=-2 into the first equation and find the value of y to get a second point:

`y=-2+3=1`

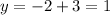
Hence, the line also passes through the point (-2,1).

Plot the points on the coordinate plane and join them with a straight line as shown below:

Next, graph the second line using the same procedure as the first:

Locate the point of intersection:

The point of intersection is (-3,0).

Hence, the solution to the system of equations is (x,y)=(-3,0), that is, x=-3, y=0.

The solution is x=-3 and y=0.