Answer:
The area of BEA is 200 square units.
Explanation:
Given information: AB||CD and CD:BA = 6:5.
Let the length of sides CD and BA are 6x and 5x respectively.
If a transversal line intersect two parallel lines, then the alternative interior angles are equal.
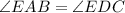 (Alternate interior angles)
(Alternate interior angles)
 (Alternate interior angles)
(Alternate interior angles)
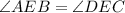 (Vertically opposite angles)
(Vertically opposite angles)
By AAA property of similarity,
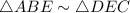
The area of two similar triangles is proportional to the square of their corresponding sides.
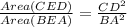
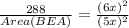

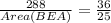
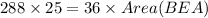

Divide both sides by 36.
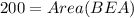
Therefore the area of BEA is 200 square units.