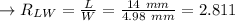Question

With a wooden ruler, you measure the length of a rectangular piece of sheet metal to be 14 mm. With micrometer calipers, you measure the width of the rectangle to be 4.98 mm. Give your answers to the following questions using the correct number of significant figures.

What is:

a. the area of the rectangle.
b. the ratio of the rectangle’s width to its length.
c. the perimeter of the rectangle.
d. the difference between the length and the width.
e. the ratio of the length to the width.

Answer 1

Follows are the solution to the given question:

Step-by-step explanation:

The rectangular part has a length of
`14 \ mm` and its rectangular part has a width of
`4.98 \ mm`.

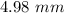In option A

Calculating the area of the rectangular throgh the given piece:

`\to A_R = WL=(14 mm) (4.98 mm) =69.72 \ mm^2`

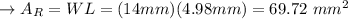
In option B

Calculating the ratio of rectangle's width which is rectangle's length:

`\to R_(WL)=(W)/(L)= (4.98 \ mm)/(14 \ mm) = 0.3557`

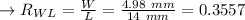
So, the ratio of rectangle's width to rectangle's length is 0.3557 .

In option C

Calculating the Perimeter of the rectangle:

`\to P_R=2(W+L)=2(14 \ mm+ 4.98 \ mm)= 2(18.98) = 37.96 \ mm`

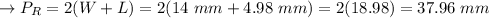
In option D

Calculating the difference between length and width:

`\to D_(LW) = L- W = 14\ mm -4.98 \ mm =9.02 \ mm`

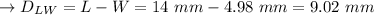
In option E

Calculating the ratio of length to width:

`\to R_(LW)=(L)/(W) =(14\ mm)/(4.98 \ mm) = 2.811`