Question

Find the length of the hypotenuse:

Answer 1

Method 1:

The sides of a right-angle triangle are equal when the angle = 45°


`a^2 = b^2 + c^2 \\ a^2 = (3 √( 2 ))^2 + (3 √( 2 ))^2 \\ a^2 = 9 * 2 + 9 * 2 \\ a^2 = 36 \\ a = \sqrt {36} = 6`

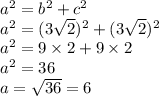
Method 2:
(Optional)

Using TOA CAH SOH method

Where:

TOA is Tan θ = Opposite/Adjasent
CAH is Cos θ = Adjasent/Hypotenuse
SOH is Sin θ = Opposite/Hypotenuse

You have an angle of 45° and OPPOSITE the angle is a known length.

These are the 2 information we know.

We need to find the third information, which is the HYPOTENUSE.

Notice the capatialised words start with the letter O ans H?

Find in the TOA CAH SOH the corresponding letters, in this case SOH.

SOH is sin θ = opposite/hypotenuse

Simply substitude in the values and find the hypotenuse!

sin 45° = (3√2)/ hypotenuse
hypotenuse = (3√2) / sin 45° = 6

Answer is B.

And there you go! Both methods can be used and gives the same answer.

However the limitations to method 2 are:

1. It must be a right-angle triangle
2. An angle and a side must be given.


If you think method 2 is too confusing, stick to method 1.

Good luck!

Answer 2

to find the hypotenuse on the given triangle

divide the given height ( 3sqrt(2) ) by the sin of the given angle (45)

3sqrt(2) / sin 45 = 6

answer is B. 6