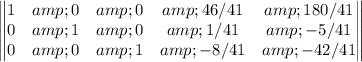Question

For the system of equations that follows, use Gaussian elimination to obtain an equivalent system whose coefficient matrix is in row echelon form. Indicate whether the system is consistent. If the system is consistent and involves no free variables, use back substitution to find the unique solution. If the system is consistent and there are free variables, transform it to reduced row echelon form and find all solutions.

x₁ + 3x₂ + x₃ + x₄ = 3;
2x₁ - 2x₂ + x₃ + 2x₄ = 8;
x₁ - 5x₂ + x₄ = 5

Answer 1

`\begin{Vmatrix}1 & 0 & 0& 46/41 &180/41\\0 & 1 & 0&1/41 &-5/41\\0&0 & 1 & -8/41& -42/41\end{Vmatrix}`

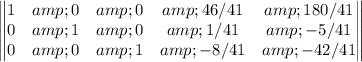
Explanation:

From the question we are told that

System of equations given as

x₁ + 3x₂ + x₃ + x₄ = 3;

2x₁ - 2x₂ + x₃ + 2x₄ = 8;

x₁ - 5x₂ + x₄ = 5

Matrix form

`\begin{Vmatrix}1 & 3 & 1&1&3\\2 & -2 & 1&2&8\\0&1 & -5 & 1& 5\end{Vmatrix}`
`\begin{Vmatrix}x_1\\x_2\\x_3\\x_4\end{Vmatrix}`

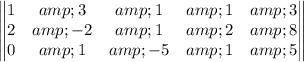
Generally the echelon reduction is mathematically applied as

`\begin{Vmatrix}1 & 3 & 1&1&3\\2 & -2 & 1&2&8\\0&1 & -5 & 1& 5\end{Vmatrix}`

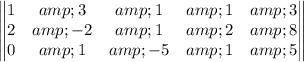
Add -2 times the 1st row to the 2nd row

`\begin{Vmatrix}1 & 3 & 1&1&3\\0 & -8 & -1&0&2\\0&1 & -5 & 1& 5\end{Vmatrix}`

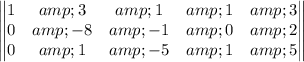
Multiply the 2nd row by -1/8

`\begin{Vmatrix}1 & 3 & 1&1&3\\0 & 1 & 1/8&0&-1/4\\0&1 & -5 & 1& 5\end{Vmatrix}`

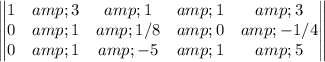
Add -1 times the 2nd row to the 3rd row

`\begin{Vmatrix}1 & 3 & 1&1&3\\0 & 1 & 1/8&0&-1/4\\0&0 & -41/8 & 1& 21/4\end{Vmatrix}`

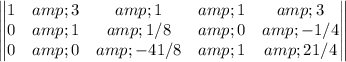
Multiply the 3rd row by -8/41

`\begin{Vmatrix}1 & 3 & 1&1&3\\0 & 1 & 1/8&0&-1/4\\0&0 & 1 & -8/41& -42/41\end{Vmatrix}`

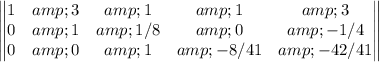
Add -1/8 times the 3rd row to the 2nd row

Add -1 times the 3rd row to the 1st row

`\begin{Vmatrix}1 & 3 & 0&49/41&165/41\\0 & 1 & 0&1/41 &-5/41\\0&0 & 1 & -8/41& -42/41\end{Vmatrix}`

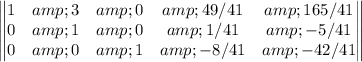
Add -3 times the 2nd row to the 1st row

`\begin{Vmatrix}1 & 0 & 0& 46/41 &180/41\\0 & 1 & 0&1/41 &-5/41\\0&0 & 1 & -8/41& -42/41\end{Vmatrix}`