Question

(c) Hence, or otherwise, find solutions of the following equations or explain why a solution does not exist.

(i) a = 273−1 mod 3019
(ii) 273b ≡ 15 (mod 3019)
(iii) 16c ≡ 1 (mod 273)
(iv) d ≡ 1 (mod 273) and d ≡ 15 (mod 3019)

Answer 1

`a\equiv273^(-1)\pmod{3019}\iff273a\equiv1\pmod{3019}`

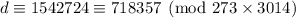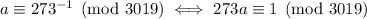
will have a solution if and only if
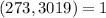
`(273,3019)=1` (coprime), which is true since 3019 is prime. So we can apply Euclid's algorithm:


`3019=273*11+16`

`273=16*17+1`

`\implies1=273-16*17`

`\implies1=273-(3019-273*11)*17`

`\implies1=273*188-3019*17`


`\implies1\equiv273*188\pmod{3019}`

`\implies a=188`

- - -


`273b\equiv15\pmod{3019}`

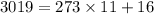
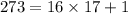
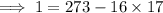
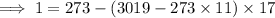
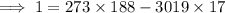
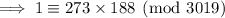
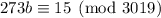
We can start off by finding the inverse of 15 via Euclid's algorithm. Let
`x` be an integer such that


`15x\equiv1\pmod{3019}`

Then


`3019=15*201+4`

`15=4*3+3`

`4=3*1+1`

`\implies1=4-3`

`\implies1=4-(15-4*3)=4*4-15`

`\implies1=(3019-15*201)*4-15=3019*4-15*805`

`\implies1\equiv15*(-805)\equiv15*2214\pmod{3019}`


`\implies15^(-1)\equiv2214\pmod{3019}`

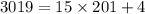
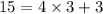
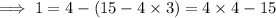
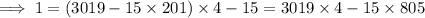
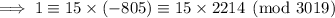
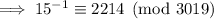
Now, multiplying both sides of the equivalence by 2214, we have


`273*2214\equiv604422\equiv622\pmod{3019}`

`\implies2214*273b\equiv2214*15\pmod{3019}`

`\implies622b\equiv1\pmod{3019}`

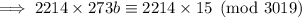
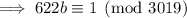
Using Euclid's algorithm, you'd end up with
`b=2820`.

- - -


`16c\equiv1\pmod{273}`

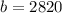
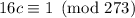
will have a solution so long as
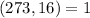
`(273,16)=1`, which is true. Use Euclid's algorithm and you should get
`c=256`.

- - -


`\begin{cases}d\equiv1\pmod{273}\\d\equiv15\pmod{3019}\end{cases}`

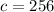
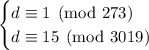
If
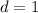
`d=1`, then surely
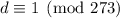
`d\equiv1\pmod{273}`, but the second equation is not satisfied. Similarly, if
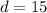
`d=15`, we do get
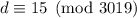
`d\equiv15\pmod{3019}`, but then the first condition is not met.

So suppose we take


`d=1*3019+273*15=7114`

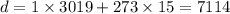
Now
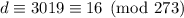
`d\equiv3019\equiv16\pmod{273}`. To get a remainder of 1, we can use the result from part (iii) and multiply the first term by 256.


`d=1*3019*256+273*15=776959`

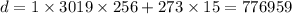
Now
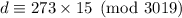
`d\equiv273*15\pmod{3019}`. From part (i), we have
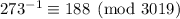
`273^(-1)\equiv188\pmod{3019}`, so we can multiply the second term by 188 to get the right remainder.

So finally,


`d=1*3019*256+273*15*188=1542724`

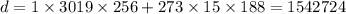
The smallest positive integer
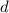
`d` that satisfies this equation would then be


`d\equiv1542724\equiv718357\pmod{273*3014}`