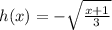Question

What is the inverse of the function h(x) = 3x^2 - 1?

Answer 1

There is a simple rule to find the inverse of any function:
1. Trade places between y and x (h(x) and x in this case)
2. Solve for y (h(x) in this case)
3. That's all!
Let's solve it now:
1. Trade places between h(x) and x:
`x = 3(h(x))^(2) -1`
2. Solve for h(x):

`3(h(x))^(2) = x+1 \\ (h(x))^(2) = (x+1)/(3) \\ h(x) = + \sqrt{ (x+1)/(3) }` or
`- \sqrt{ (x+1)/(3) }`
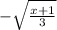
3. So, the inverse is system of graphs
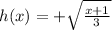
`h(x) = + \sqrt{ (x+1)/(3) }` and
`h(x) = - \sqrt{ (x+1)/(3) }`

Answer 2

Hello there!

To find the inverse, we need to interchange the variables and solve for y.

So, the answer is

`h ^(-1)(x)= \sqrt{3(1+x)/3` ,
`- √(3(1+x))/3`

I hope this helps!