Question

Find the value of x that makes m ∥ n

Answer 1

20

Explanation:

Theorem:

If two lines are cut by a transversal such that alternate interior angles are congruent, then the lines are parallel.

Lines m and n are cut by a transversal.

Angles 3x and 2x + 20 are alternate interior angles.

For lines m and n to be parallel, angles 3x and 2x + 20 must be congruent, so their measures must be equal.

3x = 2x + 20

x = 20

Answer: 20

Answer 2

The value of x that makes m || n is x = 20

Explanation:

Given a line that is intersected by another two lines (for example line ''m'' and line ''n'' like in the exercise) one of the conditions that makes m || n is that the alternate interior angles must be congruent. Understanding that congruent means the same.

In the exercise, one pair of alternate interior angles are (2x+20)° and 3x°.

We need this two angles to be congruent ⇒
`3x=2x+20`

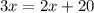
Solving this for ''x'' :

`3x=2x+20\\3x-2x=20\\x=20`

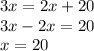
The value of x that makes 3x° congruent to 2x+20° (that makes the alternate interior angles congruents) is x = 20