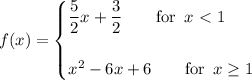Question

What's the full equation for this graph?

Answer 1

1.
Left side of a graph is a line that passes through points
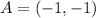
`A=(-1,-1)` and
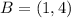
`B=(1,4)` so we can write its equation as:


`(y-y_A)=(y_B-y_A)/(x_B-x_A)(x-x_A)\\\\\\ \big(y-(-1)\big)=(4-(-1))/(1-(-1))\big(x-(-1)\big)\\\\\\ y+1=(4+1)/(1+1)(x+1)\\\\\\y+1=(5)/(2)(x+1)\\\\\\y+1=(5)/(2)x+(5)/(2)\\\\\\y=(5)/(2)x+(5)/(2)-1\\\\\\\boxed{y=(5)/(2)x+(3)/(2)}`

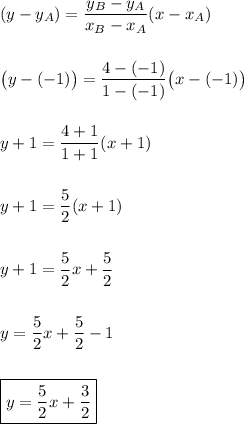
2.
Right side of a graph is a parabola with vertex
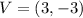
`V=(3,-3)` that passes through point
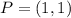
`P=(1,1)`. Its equation:


`y=a(x-x_V)^2+y_V\\\\y=a(x-3)^2+(-3)\\\\y=a(x-3)^2-3`

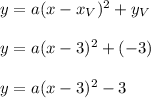
Substitute
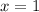
`x=1` and
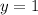
`y=1` to calculate parameter
`a`


`1=a(1-3)^2-3\\\\1=a(-2)^2-3\\\\1=4a-3\\\\4a=4\quad|:4\\\\a=1`

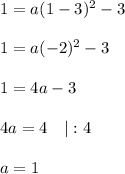
and we have the equation of parabola:


`y=a(x-3)^2-3\\\\y=1\cdot(x-3)^2-3\\\\y=(x-3)^2-3\\\\y=x^2-2\cdot x\cdot3+3^2-3\\\\y=x^2-6x+9-3\\\\\boxed{y=x^2-6x+6}`

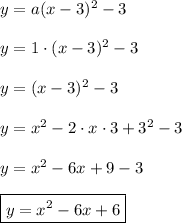
From 1. and 2. full equation for graph is:


`f(x)=\begin{cases}(5)/(2)x+(3)/(2)\qquad\text{for}\,\,\,x\ \textless \ 1\\\\x^2-6x+6\qquad\text{for}\,\,\,x\geq1\end{cases}`