Question

Sam opened a savings account with an initial deposit of $2,000. Since then, he has never made any other deposits or withdrawals. His savings account earns 0.4% interest monthly and an annual bonus of 1.5% interest. Which equation gives the approximate amount, A(x), he has in his savings account as a function of x, the number of years since his initial deposit?

A(x) ≈ 2,000 + (1.059)x3

A(x) ≈ 2,000(1.019)x2

A(x) ≈ 2,000(1.065)x

A(x) ≈ 2,000(1.059)x2

Answer 1

if my math is correct B or C is what it comes down to

Answer 2

Third option:

`A(x)\approx 2,000(1.065)^x`

Explanation:

Notice if we invest 2,000 then the first month then after the first 0.4% interest is earned we will have in the account:

2,000(1+0.004) = 2,000(1.004)

I just applied the simple interest formula.

Then after the second month we will have:

`2,000(1.004)(1.004) = 2,000(1.004)^2`

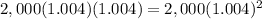
And so on each month.

So at the end of the first year (12 months) we have:

`2,000(1.004)^(12)`

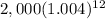
But we also earn an additional 1.5% in the year, so we will have:

`2,000(1.004)^(12)(1.015)`

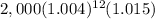
At the end of the second year we will have:

`2,000[(1.004)^(12)(1.015)]^2`

At the end of the third year:

`2,000[(1.004)^(12)(1.015)]^2`

And so on,

So if the number of years is denoted with x, at the end of x years we will have the following amount in the savings:

`2,000[(1.004)^(12)(1.015)]^x`

We use our calculator to simplify that inside the brackets:

`(1.004)^(12)(1.015)=1.06481`

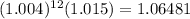
Rounding to the third decimal place we get: 1.065

So notice the amount in the savings after x years will be:

`2,000(1.065)^x`

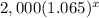
Since they want it in function notation we just write the A(x) that denotes the amount in the savings:

`A(x)\approx 2,000(1.065)^x`